return¶

Introduksjon¶

Denne uken skal vi jobbe med funksjoner i Python. La oss først de på de innebygde funksjonene i Python. Du finner en liste i Pythons dokumentasjon. Det er vel verdt å bli kjent med dokumentasjonen. Hvis du ikke kan en funksjon fra før, kan du søke den opp her og finne ut hva den gjør. Det er ikke nødvendig å lese alt dette nå, men å lese på de funksjonene du har bruk for. For nå kan det være lurt å lese på funksjonene len(), max(), min(), abs(), int(), str(), float(), round() og input().

Eksempler¶

Eksempel 1¶

Funksjoner er veldig nyttige i programmering. Blant annet lar de deg gjenbruke kodeblokker for å redusere repetisjon og feil du kan gjøre mens du programmerer, fordi funksjoner gjør at man kan kjøre samme blokk med kode flere ganger, uten å måtte skrive den samme koden flere ganger. Her er et eksempel på kode hvor vi bruker funksjoner.

I koden ser du at vi ikke nødvendigvis må kalle funksjonene i samme rekkefølge som de er definert. Som argument kan en funksjon ta ingen verdier, en eller flere verdier, og verdier med blandede typer, f.eks. int og str, som vi ser nedenfor:

Last ned filen her: eksempel_1.py.

print("----------------------")
# Function that takes no input and always returns the same value
def always_12(): # funksjonsdefinisjon
    return 12 # returnverdien


print("always_12 function:")
print(always_12()) # funksjonskall (= bruk av funksjonen)
x = always_12() + 100  # funksjonskall blir erstattet med returnverdien
print(x)



print("----------------------")


# What if we want to add 2 to a given number?
print(4 + 2)
print(7 + 2)
print(1 + 2)

# We can do this easily with a function instead, with a single input argument (our given number)
def add_2(num):   # ubestemt funksjonsargument "num", blir fylt ut når vi bruker funksjonen
    return num + 2 # kan bruke num inni funksjonen, men er ikke definert utenfor


print("add_2 function:")
print(add_2(4))  # num blir sett til 4, og så erstattes funksjonskall med return-verdi
print(100 + add_2(7) + 900) # num blir sett til 7 og så erstattes funksjonskall med return-verdi


print("----------------------")


# multi-input function with only integers
def add_2_multiply(add, mult):
    return (2 + add) * mult


print("add_multiply function:")
print(add_multiply(2, 4))
n = 5
print(add_multiply(8, n))
print(add_multiply(n, n+n)) # funksjonsargumenter kan være hva som helt uttrykk



print("----------------------")

# multi-input function with mixed type inputs
def mixed(word, num, punct):
    result = f"{word}{punct}" * num
    return result


print("mixed type input function:")
print(mixed("Hello", 2, "!"))
print(mixed("What", 5, "?"))

Eksempel 2¶

I dette eksempelet skal vi bruke flere funksjoner sammen for å bestille kaffe og kjeks. Først den samme som tidligere for å si hallo, og så en ny funksjon for å bestille mat.

Legg merke til at make_order kaller de andre funksjonene med ulike argumenter, og bruker resultatene.

Last ned filen her: eksempel_2a.py.

print("--------------------------------------")


def hello(name):
    """Greet a person nicely"""
    text = f"Hello, {name}!"
    return text


print("Print result of hello function with Alice as input:")
print(hello("Alice"))

print("--------------------------------------")


def order(food, number):
    """Make an order of one type of food"""
    return f"{number} {food}s"


print("Print result of order function with food: coffee and number: 3 as inputs:")
print(order("coffee", 3))

print("--------------------------------------")


def make_order(name, coffee_number, cookie_number):
    """Make an order of coffee and cookies"""
    greeting = hello(name)
    coffee_order = order("coffee", coffee_number)
    cookie_order = order("cookie", cookie_number)

    return f"{greeting}\nCan I have {coffee_order} and {cookie_order}, please?"


print("Lets call make_order(2, 10) to order 2 coffees and 10 cookies from Alice:")
print(make_order("Alice", 2, 10))

Hvordan bruker vi disse tre funksjoner sammen? Skjønner du hvordan resultaten fra de andre funskjonene gjenbrukes?

Her er et annet eksempel på å bruke to funksjoner sammen eksempel_2b.py.

# Change recipe to call for measurement in grams instead of cups
print("--------------------------------------")
print("An American recipe calls for 2 cups of flour. How much is this in grams?")

# first function
def cups_to_grams(cups):
    return cups * 136


# second function
def flour_text(grams):
    statement_grams = f"This recipe calls for {grams}g of flour"
    return statement_grams


# chaining first and second function together:
chained_output = flour_text(cups_to_grams(2))

print(chained_output)

Hvordan brukes den første funskjonen i den andre funksjonen?

Eksempelene her også bruker «docstrings» (documentation strings). Dette er teksten som står inne i trippel-quotes """ helt i begynnelsen av en funksjon. Docstrings forklarer hva funksjonen gjør og kan brukes av andre programmer. Prøv for eksempel å muse over funksjonsnavnene i VScode.

Eksempel 3¶

Funksjoner kan også brukes for å gjøre matematiske beregninger. Mange ganger vil man gjøre samme beregning flere ganger. Da er det lurt å plassere koden for beregningen i en funksjon som man siden kan kalle flere ganger. Om man vil gjøre flere ulike beregninger etterpå hverandre kan man dessuten gjøre det. Her er et eksempel på kode hvor vi bruker funksjoner for å regne ut lengden til hypotenusen i en rettvinklet trekant og gjennomsnittet av tre tall.

Last ned filen her: eksempel_3.py.

# Her henter vi en funksjon for å regne ut kvadratrøtter
from math import sqrt

# extract common text so a varaible
def hypotenus(katet_1, katet_2):
    """Beregn hypotenusen fra to kateter"""
    hyp = sqrt(katet_1 ** 2 + katet_2 ** 2)
    return hyp


common_text = "Lengden av hypotenusen på den rettvinklete trekanten med katetlengdene"
print(common_text, "4 og 1 er", hypotenus(4, 1))

a = 3
b = 4
print(f"{common_text} {a} og {b} er {hypotenus(a, b)}")

c = 7
d = 2
print(f"{common_text} {c} og {d} er {hypotenus(c, d)}")


def middelverdi(a, b, c):
    """Beregn middelverdi av tre tall"""
    mv = (a + b + c) / 3
    return mv


# Kan du omskrive de neste linjene med mindre repetisjon?
print(f"Middelverdien av tallene 17, 3 og 25 er {middelverdi(17, 3, 25)}")
print(f"Middelverdien av tallene 24, 72 og 13 er {middelverdi(24, 72, 13)}")
resultat = middelverdi(92, 64, 89)
print(f"Middelverdien av tallene 92, 64 og 89 er {resultat}")


# Vi kan bruke disse funksjoner (middelverdi og hypotenus) sammen
mv_hyp = middelverdi(hypotenus(4, 1), hypotenus(3, 4), hypotenus(7, 2))
print(f"Middelverdien av hypotenusene ovenfor er {mv_hyp}")

Kjør koden. Ble outputen hva du hadde ventet deg? Kan du lage noen funksjoner til, for å unngå repetisjonen i print-linjene?

Eksempel 4¶

I dette eksempelet bruker vi en funksjon for en beregning og en funksjon for å lage en streng. Vi beregner og printer andregradspolynomer.

Last ned filen her: eksempel_4.py.

def poly_string(a, b, c):
    """Create a string representation ax^2 + bx + c"""
    return f"{a} x^2 + {b} x + {c}"


def poly_value(a, b, c, x):
    """Calculate the value of ax^2 + bx + c at the point x"""
    square = a * x ** 2
    linear = b * x
    const = c
    return square + linear + const


def pretty(a, b, c, x):
    """Calculate and print a quadratic polynomial"""
    poly = poly_string(a, b, c)
    value = poly_value(a, b, c, x)
    return f"The value of {poly} for x = {x} is {value}"


print(pretty(2, 7, 3, 3))
print(pretty(4, 5, 2, 9))

Her brukes return i poly_string(). Prøv å endre koden slik at poly_string() printer strengen, i steden for å bruke return. Hva skjer?

Eksempel 5¶

Det er mulig å definere en funksjon i Python uten å bruke return. Da returnerer Python verdien None i bakgrunnen. Husk at om du vil gi verdien fra en funksjon til en annen funksjon må du bruke return.

Last ned filen her: eksempel_5.py.

# Difference in assigning a variable vs printing a variable

print("----------------")
x = 50

print("================")
y = print(50)

print("----------------")

print(f"The value of x is: {x}")
print(f"The value of y is: {y}")

Hva er forskjellen på x og y?

Hvis vi skal bruke 50 igjen seinere i programmet, burde vi se på x eller y?

Eksempel 6¶

Funksjoner uten return (de har return-verdien None) brukes ofte for å gruppere instrukser som hører sammen, og skal gjenbrukes flere ganger. Nå kan vi endre på ting på et sted og vi får den endringen med der funksjonen er brukt. Om vi hadde kopiert instruksjonene flere ganger uten å bruke en funksjon måtte vi fikset hver enkel kopi.

Last ned filen her: eksempel_6.py.

# Functions can also be used to keep related instructions together
# allowing them to be reused consistently, e.g. to make "drawings"
def ascii_wave():
    """Print an ascii wave"""
    print("\\" * 40)
    print("/" * 40)
    print("\\" * 40)


def ascii_cat():
    """Print an ascii cat"""
    print(" /\_/\\")
    print("( o.o )")
    print(" > ^ <")


def ascii_cube():
    """Print an ascii cube"""
    print("+------+.")
    print("|`.    | `.")
    print("|  `+--+---+")
    print("|   |  |   |")
    print("+---+--+.  |")
    print(" `. |    `.|")
    print("   `+------+")


def ascii_castle():
    """Print an ascii castle"""
    print(" _   |~  _")
    print("[_]--'--[_]")
    print('|\'|""`""|\'|')
    print("| | /^\\ | |")
    print("|_|_|I|_|_|")


print()
print("Here is a cat:")
ascii_cat()

print()
print("Here are two cats:")
ascii_cat()
ascii_cat()

print()
print("We can also print a castle:")
ascii_castle()


print()
print("Or a cat on a wave:")
ascii_cat()
ascii_wave()

Kjør koden. Hvorfor blir ikke ascii_cube() skrevet ut?

Obs

Noen steder i koden er det brukt en ekstra \. Se for eksempel på ascii_castle(). Her står det \' noen steder, men når vi kjører programmet printes ikke \. Dette er fordi \ er en så kalt ’escape character’. Vi kan bruke \ før tegn som ellers ville ha noen annen betydning i en streng. For eksempel, om vi ikke hadde brukt \ før ' ville Python trodd at strengen var slutt ved ' og vi hadde fått en feilmelding (prøv gjerne). Men når vi putter \ før ' sier vi til Python at vi ikke mener at strengen er slutt her, uten at Python skal printe tegnet '. Siden \ er et spesielt tegn på denne måten må vi bruke \ før \ om vi vil at Python skal lese strengen som tegnet \ og ikke som en escape character. Det er derfor det står \\ på alle steder hvor vi vil printe \. Du kan lese mer om escape characters her, og her er en liste med eksempler på alle escape characters i Python 3.

Eksempel 7¶

Her er et eksempel på hva som skjer om man ikke bruker return i funksjoner.

Hva om vi vil lagre resultatet i en variabel? For eksempel, hvis vi vil huske navnet fra tidligere funksjon hello kan vi lagre resultatet i myName. I eksempelet er det to funksjoner: hello1 og hello2. hello1 bruker print() mens hello2 bruker return i slutten av funskjonen.

Last ned filen her: eksempel_7.py.

# Function using print()
def hello_printed(name):
    """Greet a person nicely"""
    text = f"Hello, {name}! How are you?"
    print(text)
    print("you do not see me until this function is called")


myName_1 = hello_printed("Ola")
print(f"hello_printed gives us: {myName_1}")  # Why does this give None?

# Same function, but using return statement instead to store the result of the function
def hello_ret(name):
    """Greet a person nicely"""
    text = f"Hello {name}! How are you?"
    return text


myName_2 = hello_ret("Ola")
print(f"hello_ret gives us: {myName_2}")

Kjør koden. Hva er forskjellen på hello1 og hello2? Hva lagres i myName?

Det er ikke vanlig å ha med print() i en funksjon som skal regne ut noe. Returner verdien eller en streng i steden for. Da kan brukeren til funksjonen bestemme om det skal printes noe eller om verdien skal gjenbrukes på en annen måte.

Eksempel 8¶

Last ned filen her: eksempel_8.py.

def avstand(tall_1, tall_2):
    """Regn ut avstand mellom to tall"""
    avst = abs(tall_1 - tall_2)
    print(avst)


def den_er_feil():
    """Denne funksjonen skulle ikke kjøre, men det fungerer uansett?"""
    abc = 5
    return xyz  # forventer NameError... her


print("vvvvvvvvvvvvvvvv")

avst_1 = avstand(14, -9)
avst_2 = avstand(-36, 23)

print("Avstanden mellom tallene 14 og -9 er", avst_1)
print("Avstanden mellom tallene -36 og 23 er", avst_2)

print("Den største av disse avstandene er", max(avst_1, avst_2))

print("^^^^^^^^^^^^^^^^")

Når du prøver å kjøre koden får du en feilmelding.

Se på det vanlige outputet før feilmeldingen: hvorfor ser det slik ut?
Hvorfor får du error når du kjører koden?
Hvorfor blir ikke den siste raden skrevet ut?
Endre koden slik at den kjører.
Hvorfor fikk du ingen feilmelding fra den_er_feil()-funksjonen?

Oppgaver¶

I disse oppgavene skal du lage og bruke funksjoner.

Advarsel

Ikke bruk input() i koden din, untatt oppgave 10, fordi da vil autotestene ikke kjøre.

Oppgave 1¶

I filen uke_05_oppg_1.py, skriv en funksjon som heter multiply_3(). Funksjonen skal ta et argument (av typen `int), multiplisere dette med 3, og returnere resultatet. Det er ikke nødvendig å printe ut resultatet.

def multiply_3(my_number):
    # din kode her

Oppgave 2¶

Nå skal vi prøve et likt problem som oppgave 1, men denne tiden med strings. I filen uke_05_oppg_2.py, skriv en funksjon som heter make_question(). Funksjonen skal ta et argument (av typen str), legge til en "?" til slutten av ordet eller frasen, og returnere resultatet. For eksempel, argumentet "Hello" skal returnere "Hello?".

Ikke ta input fra brukeren, bare lag funksjonen. Om du vil sjekke den, kan du f.eks printe den med ulike argumenter:

def make_question(text):
    # din kode her

print(make_question("Hello"))
print(make_question("How are you"))

Oppgave 3¶

I filen uke_05_oppg_3.py, skriv en funksjon som heter name_age(). Funksjonen skal ta to argumenter: (1) navnet til en person og (2) personens alder. Navnet er en str og alderen er int. Funksjonen skal returnere en streng med setningen "{navn} er {alder} år gammel." (NB: uten krøllparenteser!).

For eksempel, name_age("Ola", 7) skal returnere strengen "Ola er 7 år gammel."

Oppgave 4¶

I filen uke_05_oppg_4.py, skriv en funksjon som heter my_math(). Funksjonen skal ta to argumenter $a$ og $b$ og skal returnere $2 a + b$ .

Oppgave 5¶

I denne oppgaven skal vi lage våre egne funksjoner som beregner maximum, minimum og absoluttverdi av to tall. Vi skal også beregne lengden til en streng.

Vi skal sammenligne disse med Pythons innebygde funksjoner max(), min(), abs() og len().

I filen uke_05_oppg_5.py, skriv kode som gjør følgende:

Definerer en funksjon som heter egen_abs() som beregner absoluttverdien til et tall $a$ uten å bruke abs(). Du kan for eksempel bruke if.
Definerer en funksjon som heter egen_max() som beregner maximum av heltallene $a$ og $b$ ifølge formelen:

$\frac{a + b + | a - b |}{2} .$

( $| a - b |$ betyr absoluttverdien av $a - b$ .) Funksjonen skal returnere et heltall.
Definerer en funksjon som heter egen_min() som beregner minimum av heltallene $a$ og $b$ ifølge formelen:

$\frac{a + b - | a - b |}{2} .$

Funksjonen skal returnere et heltall.
Definerer en funksjon som heter egen_len() som beregner lengde til en streng uten å bruke len(). (Tips: bruk en løkke.)

Prøv å kjøre koden din med noen ulike tall. Gir dine egne funksjoner riktig svar?

Ikke vurdert: Kan du implementere din egen round(x, n)?

Oppgave 6¶

I denne oppgaven skal vi fortsette med min() og max(), med denne gangen skal vi identifisere den eldste av to mennesker. I filen uke_05_oppg_6.py skriv en funksjon som heter hvem_eldst() som tar som input fire argumenter: navnet på første personen (string), alderen på første personen (int), navnet på andre personen (string), alderen på andre personen (int). Funksjonen bestemmer siden hvem som er eldre og returnerer en setning som angir navn og alder på den eldste personen enligt følgende eksempel: hvem_eldst("Ola", 43, "Katrine", 23) skal returnere strengen "Ola er 43 år og eldst."

Oppgave 7¶

Den Hydrostatiske Balansen - Del I

Trykket (P) i atmosfæren og i det indre hav kan i en første tilnærming beskrives som hydrostatisk. Trykket (i enheten Pascal), som en partikkel plassert på en dybde $z$ i havet er utsatt for gis av følgende formel:

P = ρ \cdot g \cdot z

hvor $ρ$ er vanndensiteten (med enheten $kg \cdot m^{- 3}$ ), $g$ er tyngdekraftens akselerasjon (med enheten $m \cdot s^{- 2}$ ) og $z$ er partikkelens dybde (med enheten $m$ ). SI-enheten for trykk er Pascal $[Pa]$ , men i meteorologi og oceangrafi blir dokk trykk vanligvis presentert i enheten decibar $[dbar]$ . Disse to henger sammen ifølge formelen: $1 Pa = 10^{- 4} dbar$ .

I filen uke_05_oppg_7.py skriv en funksjon som heter hyd_pres() og som beregner trykket på en gitt dybde i enheten $dbar$ . Argumentene til funksjonen skal være: en densitetsverdi ( $ρ$ ), tyngdekraftens akselerasjon ( $g$ ) og dybden ( $z$ ).

For eksempel, om vi bruker densiteten $ρ = 1025 kg \cdot m^{- 3}$ og tyngdeakselerasjonen $g = 10 m \cdot s^{- 2}$ så er trykket $102.5 dbar$ på dybde $100 m$ . Det betyr altså at hyd_pres(1025,10,100) skal returnere verdien $102.5$ .

Oppgave 8¶

I denne oppgaven skal vi fortsette med konverteringen fra stones og pounds til kilograms som vi gjorde uke 2 i oppgave 3, men denne gangen skal vi bruke funksjoner.

I filen uke_05_oppg_8.py skal du definere følgende funksjoner:

stones_to_pounds() som tar som argument en vekt i stones og konverterer den til en vekt i pounds ifølge formelen:

$V_{l b} = V_{s t} * 14,$

hvor $V_{l b}$ er vekten i pounds og $V_{s t}$ er vekten i stones.

stones_to_kg() som tar som argument en vekt i stones og konverterer den til en vekt i kilogram ifølge formelen:

$V_{k g} = \frac{V_{s t}}{0.15747},$

hvor $V_{k g}$ er vekten i kilogram og $V_{s t}$ er vekten i stones.
pounds_to_kg() som tar som argument en vekt i pounds of konverterer den til en vekt i kilogram ifølge formelen:

$V_{k g} = \frac{V_{l b}}{2.20462},$

hvor $V_{k g}$ er vekten i kilogram og $V_{l b}$ er vekten i pounds.
imperial_to_metric() som tar som argument en vekt i stones og en vekt i pounds og returnerer summen av disse vektene i kilogram. Rund resultatet til 2 desimalplasser. (TIPPS: Du kan gjerne bruke koden på nytt fra funksjonene du allerede har skrevet).

Oppgave 9¶

I denne oppgaven skal vi dra tilbake til uke_02 og lage en ramme rundt ut en haiku. Derimot, denne gangen vil vi skrive dette som en funksjon, og vi skal ikke bruke print() i funksjonen.

I filen uke_05_oppg_9.py, skriv en funksjon som heter draw_haiku_frame() som tar de tre radene i en haiku som tre argumenter og returnerer en streng med hele haikuen med høyrejustering og med en ramme av «@» runt.

For eksempel, om vi printer resultatet av draw_haiku_frame("What a pleasure to", "Right justify a haiku", "As an exercise") skal vi få følgende output:

@@@@@@@@@@@@@@@@@@@@@@@@@
@    What a pleasure to @
@ Right justify a haiku @
@        As an exercise @
@@@@@@@@@@@@@@@@@@@@@@@@@

(Tips: bruk len() og max() til å finne lengden av den lengste raden. Siden printer du hver rad med så mange mellomrom før raden som det er forskjell mellom den raden og den lengste raden i haikun. Husk å printe en rad med «@» før og etter haikuen og husk å printe «@» i starten og slutten av hver rad med tekst. Hvor mange tegn lengre må toppen og bunnen av rammen være enn den lengste raden i haikuen?)

Oppgave 10¶

I filen uke_05_oppg_10.py skal vi finne (den innvendige) tangeringssirkelen til en trekant. Tangeringssirkelen er den største sirkelen som får plass inne i en trekant, se bilde:

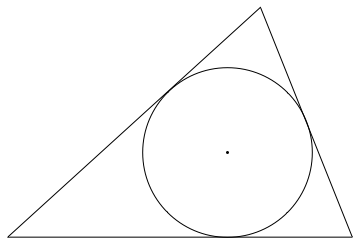
Vi får gitt de tre hjørnene i triangelen (hver hjørne består av en x-koordinat og en y-koordinat) og så skal vi beregne mittpunkten og radiusen på tangeringssirkelen.

Start med å laste ned filen uke_05_oppg_10_skeleton.py (du må døpe om filen til uke_05_oppg_10.py):

from math import sqrt


def side_length(x1, y1, x2, y2):
    """Returns the length of the side between the points (x1,y1) and (x2,y2)"""
    # din kode her


def mid(x1_or_y1, x2_or_y2, x3_or_y3, a, b, c):
    """
    Returns midpoint coordinate given:
    coordinates x1_or_y1, x2_or_y2, x3_or_y3
    and sidelengths a (opposite (x1,y1)), b (opposite (x2,y2)), c (opposite (x3,y3))
    """
    # din kode her


def incircle_radius(a, b, c):
    """Returns the radius of the incircle of a triangle with sidelengths a, b and c"""
    # din kode her


def find_incircle(x1, y1, x2, y2, x3, y3):
    """
    Finds and prints the center and radius of the incircle
    of a triangle with corners (x1,y1), (x2,y2), (x3,y3)
    """

    print(f"Your triangle is ({x1}, {y1}), ({x2}, {y2}), ({x3}, {y3}).\n")

    print("First we calculate the sidelengths.")
    side1 = 0  # side opposite (x1,y1)
    side2 = 0  # side opposite (x2,y2)
    side3 = 0  # side opposite (x3,y3)

    print("Then we find the center.")
    center_x = 0
    center_y = 0
    print(f"The center is {center_x, center_y}.\n")

    print("Finally we calculate the radius of the incircle.")
    radius = 0
    print(f"The incircle has radius {radius}.")


print("Define your triangle:")
x1 = int(input("x1 = "))
x2 = int(input("x2 = "))
x3 = int(input("x3 = "))

y1 = int(input("y1 = "))
y2 = int(input("y2 = "))
y3 = int(input("y3 = "))

find_incircle(x1, y1, x2, y2, x3, y3)

For å finne tangeringssirkelen er det ganske mange ting vi må regne ut, men ved å bryte problemet ned til mindre funksjoner og sette dem sammen blir det enklere å løse.

Den første funksjonen heter side_length(). Bytt ut kommentaren # Din kode her med kode som beregner lengden på siden mellom punktene $(x 1, y 1)$ og $(x 2, y 2)$ . Lengden $l$ gis av formelen:

l = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}

Tips: du kan bruke sqrt() til å regne ut kvadratrot.

Neste funksjon er mid(). Her skal vi beregne midtpunkten av trekanten. Vi må gjøre det hver for seg for x-koordinaten og for y-koordinaten.

Midtpunktens x-koordinat gis av formelen:

x = \frac{x_{1} \cdot a + x_{2} \cdot b + x_{3} \cdot c}{a + b + c},

og midpunktens y-koordinat gis av formelen:

y = \frac{y_{1} \cdot a + y_{2} \cdot b + y_{3} \cdot c}{a + b + c},

hvor $a$ er lengden av siden som er motsatt $(x_{1}, y_{1})$ , $b$ er lengden av siden som er motsatt $(x_{2}, y_{2})$ og $c$ er lengden av siden som er motsatt $(x_{3}, y_{3})$ (fra wikipedia).

Siden disse to formlene er veldig like (vi bare bytter ut x-koordinater mot y-koordinater) så kan vi bruke én funksjon for å finne både midpunktens x-koordinat og y-koordinat. Dette er hva funksjonen mid() skal gjøre. Den tar enten x-koordinatene til triangelens hjørner og sidlengdene og beregner midpunktens x-koordinat, eller y-koordinatene til triangelens hjørner og sidlengdene og beregner midpunktens y-koordinat.

Funksjonen incircle_radius() skal beregne radiusen til tangenssirkelen basert på sidelengdene a, b og c. Radiusen $r$ gis av formelen:

r = \sqrt{\frac{(s - a) (s - b) (s - c)}{s}},

hvor $s = (a + b + c) / 2$ (fra wikipedia).

Til slutt skal vi fylle inn find_incircle(). Alle stedene der det står 0 skal vi bruke funksjonene vi allerede har skrevet til å regne ut den riktige verdien. Her gjelder det å holde tunga rett i munnen og bruke de riktige punktene og sidelengdene.

Når du er ferdig, prøv å kjøre programmet og test noen forskjellige trekanter!