Uke 8 — Problemløsning¶

Eksempler¶

Vi skal se på noen eksempler på hvordan man kan løse problemer ved hjelp av programmering. Fokusen denne uken ligger på identifisering av programmeringsstrukturer: if-setninger, for-løkker, etc.

Eksempel 1¶

Først skal vi jobbe sammen i grupper for å løse oppgaven i denne lille teksten:

Du jobber med et prosjekt hvor du må sortere en gruppe mennesker i to grupper: eksperter og ikke-eksperter, basert på en egenrapportert nivå av kompetanse i et biologitema fra 0 (ikke kunnskapsrik) til 5 (ekstremt kunnskapsrik). De som har sagt nivå 4 eller 5 burde bli plassert i gruppen «eksperter» mens resten burde bli plassert i gruppen «ikke eksperter.»

Beskriv for hverande hvordan du vil løse oppgaven med programmering. Hva er forventet input? Hva skal du skrive ut? Hvor vil du bruke for-løkker, if-setninger eller funksjoner?

Det er nok å skissere en løsning, du trenger ikke å programmere noe.

Eksempel 2¶

Vi skal løse Problem 2 fra projecteuler.net:

Each new term in the Fibonacci sequence is generated by adding the previous two terms. By starting with 1 and 2, the first 10 terms will be:

\[1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...\]

By considering the terms in the Fibonacci sequence whose values do not exceed four million, find the sum of the even-valued terms.

Dette problemet kan deles opp i to deler: først må vi finne alle tall i Fibonaccisekvensen som er mindre enn fire millioner, så summerer vi alle av disse som er partall.

For å beregne Fibonaccisekvensen må vi gjøre samme ting (å addere de to forrige tallene) mange ganger. Dette er hva en loop er til for.

Vi vet ikke hvor mange ganger vi må beregne nye tall, vi vet bare at vi skal slutte når vi får et tall som er større enn fire millioner. Derfor bruker vi en while-løkke. Vi må også lagre alle tallene på noen måte. Til dette bruker vi en liste. Så vår kode skal være noe slikt:

fib = [] # Fibonaccisekvensen

fib.append(1) # Vi må ha de første to tallen i sekvensen før løkken
fib.append(2)

while n < 4000000: # n er det seneste tallet i sekvensen
    # Beregne neste tall i sekvensen
    # Putte tallet i slutten av fib

For å beregne neste tall i sekvensen skal vi addere de to forrige tallene. Derfor må vi hele tiden lagre de to forrige tallene sånn at vi kan bruke dem i neste omgang av løkken. La \(m\) være tallet før \(n\), og la \(l\) være tallet før \(m\). Så for eksempel, i begynnelsen er \(l=1\) og \(m=2\). I neste omgang er \(l=2\) og \(m=3\) etc. Vi bruker så disse for å beregne \(n\) . Vår kode blir da noe slikt:

fib = [] # Fibonaccisekvensen

l = 1
m = 2

fib.append(l) # Vi må ha de første to tallen i sekvensen før løkken
fib.append(m)

n = 0  # n må være definert før løkken

while n < 4000000: # n er det seneste tallet i sekvensen
    n = l + m
    fib.append(n)

    l = m # l og m må oppdateres
    m = n

Nå har vi alle tall i Fibonaccisekvensen som er mindre enn fire millioner. Nå må vi beregne summen av alle av disse som er partall.

Her passer det også å bruke en løkke fordi vi vil gå gjennom hele listen fib og gjøre noe: sjekke om tallet er partall, og (hvis det er et partall) addere det til summen.

Når vi vil gjøre noe for alle elementer i en liste bruker vi en for-løkke. Koden blir:

fib = [] # Fibonaccisekvensen

l = 1
m = 2

fib.append(l) # Vi må ha de første to tallen i sekvensen før løkken
fib.append(m)

n = 0  # n må være definert før løkken

while n < 4000000: # n er det seneste tallet i sekvensen
    n = l + m
    fib.append(n)

    l = m # l og m må oppdateres
    m = n


sum = 0 # Summen må være definert før løkken

for n in fib:
    if n % 2 == 0:
        sum += n

print(sum) # Sånn at vi får vite hva summen er

Du kan finne hele koden her: eksempel_fibonacci.py.

Diskuter andre løsingsforslag. Kan vi løse oppgaven uten lister? Hva er fordeler / ulemper med ulike løsninger?

Eksempel 3¶

Her skal vi lage en enkel simulasjon av en populasjonsmodell.

På en liten øy finnes \(x=400\) sauer og \(y=20\) ulver. Uten ulver vokser antallet av sauer eksponensielt over tid. Uten sauene forsvinner alle ulvene etter en stund. Når begge finnes på øyen, går antallet ulver litt opp i hvert tidsskritt, og antallet sauer går ned avhengig av hvor mange ulver og sauer det finnes.

I vårt eksempel skal tallene forendres slikt etter et tidsskritt \(\Delta t\):

\[\begin{split}\Delta x = \left( \frac{2}{3}x - \frac{1}{15}xy \right) \Delta t\\ \\ \Delta y = \left( \frac{1}{400}xy - y \right) \Delta t\end{split}\]

På hvert tidspunkt vil vi vise hvor mange ulver og sauer vi har. Vi kan bruke print for å lage et enkel søylediagram ved å skrive ut ulike antall 'x' og '.' i hvert tidsskritt.

Prøv å skissere en løsning, og diskuter med andre i din gruppe.

Så kan du se på vårt løsningsforslag her: wolf_sheep.py.

(De som er interessert kan finne mer om denne typen ligningssystemer under stikkordet Lotka-Volterra equations. )

Oppgaver¶

Oppgave 1¶

I uke_08_oppg_1.py skal du lage en funksjon som regner ut vekslepenger. Skriv en funksjon return_change(payment, price) som returnerer en liste med mynter som skal betales tilbake. Myntene er 1, 5, 10 og 20-kroner, og du vil betale tilbake med så få mynter som mulig. (du vil heller bruk én 20-kroning enn tjue 1-kroninger). Ikke bruke print() eller input() i innleveringen.

Eksempelkjøring:

 >>> return_change(30, 20)
[10]

>>> return_change(30, 13)
[10, 5, 1, 1]

Oppgave 2¶

Pearsons korrelasjonsligning er gitt av:

\[r = \frac{\sum_i (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_i(x_i - \bar{x})^2 \sum(y_i - \bar{y})^2}}\]

\((x, y)\) er tidsserier (hver er en liste med målinger) og \((\bar{x}, \bar{y})\) er de tilsvarende gjennomsnittene av hver liste.

I filen uke_08_oppg_2.py implementer Pearsons korrelasjonsligningen som funksjonen pearson_corr(x,y) som tar som argumenter to lister x og y og returnerer koeffisienten \(r\) hvor \(-1 \leq r \leq 1\). .. Funksjonen din bør konkurrere med hvert av de følgende steger: Fremgangsmåten:

Ta gjennomsnittet av \(x\) i variablen mean_x og \(y\) i variablen mean_y.
Lag listene dx and dy som inneholder forskjellene \((x_i - \bar{x})\) og \((y_i - \bar{y})\).
Multipliser hvert elements forskjell fra gjennomsnittet i x -listen med forskjellen fra gjennomsnittet i y -listen dx[i] * dy[i]. Summer disse multipliserte verdiene og lagre dem i variabelen sum_dxdy.

TIP: Du kan bruke sum() og zip() for å hjelpe med beregningen til produktet av forskjellene for hvert parvis listeelement og for å oppsummere disse resultatene.
Lag nye variabler dx2 og dy2 som summen av de kvadrerte forskjellene: dx2 \(= \sum_i(x_i - \bar{x})^{2}\) og dy2 \(= \sum_i(y_i - \bar{y})^{2}\).
Multipliser dx2 og dy2 og ta kvadratroten til produktet. Lag resultatet i variabelen sqr_dx2dy2.
Til slutt, beregne korrelasjonskoeffisienten r som divisjon av sum_dxdy med sqr_dx2dy2. Variabelen r er resultatet som funksjonen returnerer.

Du kan teste funksjonen din med disse verdiene:

x1_ls = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
y1_ls = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
y2_ls = [1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024]

>>> pearson_corr(x1_ls, y1_ls)
1.0

>>> pearson_corr(x1_ls, y2_ls)
0.7751168025822525

Oppgave 3¶

Måltidsplanlegging for late mennesker

Du hadde en lang dag på skolen og du vil ikke dra til matbutikken på veien hjem. Du vet hva som finnes i kjøleskapet ditt og du har fire måltider som du elsker å lage ofte. Siden du tar INF100 bestemmer du deg for å lage en algoritme som finnes de måltidene som du kan lage med det du har i kjøleskapet ditt.

# contents of my fridge, in a list
my_fridge = ["tomato sauce", "mustard", "potatoes", "carrots", "chicken", "frozen fish"]

# ingredients for all 4 meals in tuple
meals = [
    # name of dish [0], ingredients [1]
    ("fish_sticks", ["frozen fish", "potatoes", "mustard"]),
    ("chicken_curry", ["chicken", "curry paste", "carrots", "potatoes", "rice"]),
    ("chicken_veg", ["chicken", "potatoes", "carrots"]),
    ("pasta", ["spaghetti", "tomato sauce"]),
]

Løs oppgaven i to steger I filen uke_08_oppg_3.py gjør følgende:

Først, implementer en funksjon som heter meal_list() som tar som input to argumenter: (1) ingredienser i kjøleskapet ditt og (2) lister av ingredienser til en måltid. Funksjonen returnerer True (du har alle ingredienser for å lage måltiden) eller False (du har IKKE alle ingredienser for å lage måltiden). Bruk kodeskissen nedenfor for å komme i gang hvis du vil.

def meal_list(fridge, ingredient_list):
  """
  1. set up a tally that counts the ingredients you do have for a given meal in your fridge
  2. _for each_ ingredient in a meal
  3. check _if_ that ingredient is in your fridge
  4. _add_ to tally of ingredients for a given meal that are in your fridge
  5. once you have looped through the ingredient list, check _if_ your count tally matches the number of items in the ingredient list
  """
  count = 0

  # skriv koden her

  return count == len(ingredient_list)

Så lag en annen funksjon som heter meal_options() for å finne måltidene du kan lage med ingrediensene du har i kjøleskapet ditt.

def meal_options(fridge, meals):
  """
  1. _for each_ tuple pair in meals
  2. run meal_list()
  3. _if_ function evaluates to `True`, then add to a new list of meals that are possible to make
  """
  meal_options_ls = []

  # your code here

  return meal_options_ls

Eksempelkjøring:

>>> meal_list(my_fridge, meals[0][1])
True

>>> meal_options(my_fridge, meals)
['fish_sticks', 'chicken_veg']

Obs

Du trenger å levere kun en av oppgavene 4, 5 eller 6 sammen med oppg.1-3.

Oppgave 4¶

I gamle egyptiske tekster finner vi en multiplikasjonsmetode for vilkårlige positive heltall, som fungerer med bare addisjon og dobling.

For å multiplisere for eksempel a = 19 og b = 23, begynner vi med å skrive 1 og doble det til det nye tallet ville vært større enn a:

Vi stopper på 16, siden 32 er større enn a = 19.

Det finnes nå ett unikt utvalg av disse tallene hvor summen resulterer i a = 19.

Det er 16 + 2 + 1. Vi markerer disse tallene med X.

I den tredje kolonnen starter vi med tallet b = 23, og fortsetter å doble.

X    1    23
X    2    46
     4    92
     8   184
X   16   368

Til slutt tar vi bare de tallene fra den siste kolonnen som er merket med X, og summerer dem:

23 + 46 + 368 = 437. Dette er vårt resultat: 19 * 23 er 437.

I uke_08_oppg_4.py skriv et program som gjør følgende:

Spør brukeren om to positive heltall med input().
Ved behov, bytt tallene slik at det første tallet er mindre enn det andre.
Regn ut innholdet til den egyptiske multiplikasjonstabellen etter fremgangsmåten som er vist ovenfor.
Skriv ut den ferdige multiplikasjonstabellen med pen formatering og justerte kolonner; slik at den ser ut som eksemplene vist nedenfor.

For formateringen kan du anta at brukeren bare gir deg tall mellom 1 og 99.

Programmet trenger å kjøre bare en gang hver gang det startes, du trenger ikke å be om nye input etter utskriften.

Noen eksempler på programkjøring ser slik ut:

Factor A: 10
Factor B: 13
=========================
    1   13
X   2   26
    4   52
X   8  104
=========================
2 + 8 = 10
26 + 104 = 130
=========================
10 * 13 = 130

Factor A: 19
Factor B: 23
=========================
X    1   23
X    2   46
     4   92
     8  184
X   16  368
=========================
1 + 2 + 16 = 19
23 + 46 + 368 = 437
=========================
19 * 23 = 437

Factor A: 17
Factor B: 6
=========================
     1   17
X    2   34
X    4   68
=========================
2 + 4 = 6
34 + 68 = 102
=========================
17 * 6 = 102

Obs

Du trenger å levere kun en av oppgavene 4, 5 eller 6 sammen med oppg.1-3.

Oppgave 5¶

Hordaland har 15 distriktsmandater i Stortinget. Disse 15 mandatene skal fordeles mellom partiene i forhold til stemmetallet de fikk. Metoden er beskrevet slikt i valgloven §11-4 (3):

Hver partiets stemmetall divideres med 1,4 - 3 - 5 - 7 osv. Hvert stemmetall skal divideres så mange ganger som det er nødvendig for å finne det antall mandater listen skal ha. Det første mandatet tilfaller den listen som har den største kvotienten. Det andre mandatet tilfaller den listen som har den nest største kvotienten osv.

Et eksempel på en mandatsfordeling av 11 seter (fra regjeringen.no):

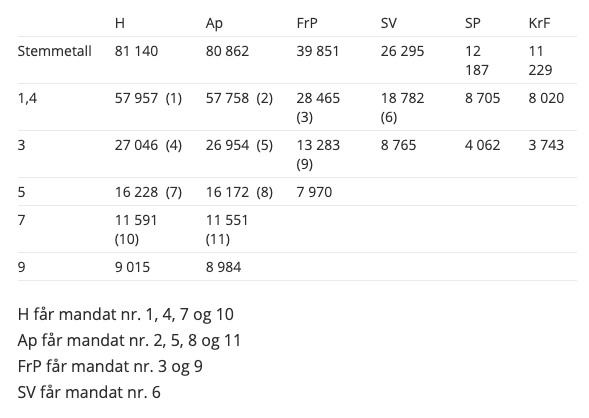
I uke_08_oppg_5.py må du lage 3 funksjoner som bygger på hverandre:

valgresultat(parties, votes, seats),
parti_mandater(party_list, votes, seats) og
pretty(mandater):

Først lag en funksjon valgresultat(parties, votes, seats) som tar som argumenter (1) listen av partier, (2) listen med stemmer til hvert parti og (3) antallet mandater som skal fordeles. Funksjonen skal returnere en liste av seats tupler som viser kvotienten som float og partinavnet, f.eks:

parties = ["H", "Ap", "FrP", "SP", "SV", "KrF", "R", "V", "MdG"]
votes = [74282, 68945, 38352, 29981, 26901, 14724, 14150, 13163, 11940]
N_seats = 15

print(valgesultat(parties, votes, N_seats))

[(53058.571428571435, 'H'), (49246.42857142857, 'Ap'), (27394.285714285717, 'FrP'), ... ] # 15 tuples

Så lag en funksjon som heter parti_mandater(party_list, votes, seats) som igjen tar som argumenter listen av partier, listen av stemmer, og antallet mandater. Funksjonen skal gjenbruke valgesultat() internt og skal returnere en liste av tupler som viser partinavn og antallet stemmer og antallet mandater for hvert parti. Partier uten mandat skal ikke nevnes i tuplen. For eksempel, resultat i Hordaland gir følgende tuple:

[('H', 74282, 4), ('Ap', 68945, 4), ('FrP', 38352, 2), ('SP', 29981, 2), ('SV', 26901, 1), ('KrF', 14724, 1), ('R', 14150, 1)]

TIPS: Funksjonen er veldig lik oppgaven 3.

Til slutt, lag en funksjon som heter pretty(mandater) som tar resultatet fra parti_mandater() og presenterer det med pen formatering med avstanden som vist i eksempelkjøring nedenfor (tallene justert til høyre):

Parti  Stemmer  Mandater
========================
H        74282         4
Ap       68945         4
...

TIPS: Husk f-string formatering, f.eks:

print(f"{a:10}{b:6}{c:6}")

Obs

Du trenger å levere kun en av oppgavene 4, 5 eller 6 sammen med oppg.1-3.

Oppgave 6¶

Skriv i filen uke_08_oppg_6.py en funksjon justify som fyller ut en tekst med mellomrom slik at alle rader får samme lengde. Lengden på radene skal være et argument til funksjonen. Den justerede teksten skal returneres av funksjonen som en streng. Funksjonen skal ikke bruke print() eller input(). Her er hele spesifikasjonen:

Input: justify skal ta to argument, en str (text) og en int (line_len).

Output: funksjonen skal returnere samme tekst som i text men hvor alle rader har lengden line_len.

Vilkår:

Alle rader må inneholde så mange ord som er mulig innen radlengden.
Funksjonen får bare fylle ut med mellomrom (’ ’) mellom ordene (ikke tab eller noen annen whitespace).
Mellomrommen i hver rad må være så jevnt fordelt som mulig, i.e. forskjellen mellom størst antall mellomrom og minst antall mellomrom mellom ordene i en rad får ikke være mer enn 1. Men du får selv velge hvordan du vil plassere ut mellomrommen så lenge dette er oppfyllt.
Alle rader må begynne med et tegn som ikke er whitespace.
Slutten på alle rader må enten være på formen 'char\n' eller 'char', hvor 'char' er et tegn som ikke er whitespace, i.e. du får ikke begynne eller slutte en rad med mellomrom.
Den siste raden i teksten skal ikke bli fylt ut med mellomrom. I denne raden skal det være eksakt ett mellomrom mellom alle ord.
Du kan anta at ingen ord i text er lengre enn line_len.

Eksempel: om input til funksjonen er følgende tekst:

Alice was beginning to get very tired of sitting by her sister
on the bank, and of having nothing to do: once or twice she had peeped
into the book her sister was reading, but it had no pictures
or conversations in it, 'and what is the use
of a book,' thought Alice 'without pictures or conversation?'

og line_len er 60 skal funksjonen returnere noe slikt:

Alice was beginning to get very  tired  of  sitting  by  her
sister on the bank, and of having nothing  to  do:  once  or
twice she had peeped into the book her sister  was  reading,
but it had no pictures or conversations in it, 'and what  is
the use of a  book,'  thought  Alice  'without  pictures  or
conversation?'

(men du får selv velge hvordan du vil plassere mellomrommene, innen vilkårene).

Uke 8 — Problemløsning¶

Eksempler¶

Eksempel 1¶

Eksempel 2¶

Eksempel 3¶

Oppgaver¶

Oppgave 1¶

Oppgave 2¶

Oppgave 3¶

Oppgave 4¶

Oppgave 5¶

Oppgave 6¶

Table of Contents

Forrige tittel

Neste emne

Denne siden